Predavanja in delavnice
printKo grafi priskočijo na pomoč
As. mag. Boštjan Frelih, UP FAMNIT
Ali lahko diagram na sliki narišemo z eno potezo, tako da svinčnik ne odmaknemo z risalne površine in vsako "črto" (ravno ali ukrivljeno) narišemo natanko enkrat? Ali lahko skakač (konj) obišče vsako polje šahovnice z zaporedjem skokov in zaključi sprehod na začetnem polju? Na taka in podobna vprašanja bomo poiskali odgovore s pomočjo rezultatov s področja matematike, ki mu pravimo teorija grafov.
Kako so računali v starih civilizacijah?
As. dr. Marjan Jerman, UL FMF in UP FAMNIT
 Poznate grški papirus, Rhindov papirus, babilonske tablice? V teh starodavnih knjižicah najdemo naloge, kot so:
Poznate grški papirus, Rhindov papirus, babilonske tablice? V teh starodavnih knjižicah najdemo naloge, kot so:
- Če sešteješ ploščino in stranico kvadrata, dobiš 3/4. Kako dolga je stranica kvadrata?
- Poišči stranice pravokotnega trikotnika, če veš, da je vsota katete in hipotenuze 8, druga kateta pa je dolga 4.
- Znamenita naloga o Arhimedovi sončni čredi.
V starih civilizacijah so brez znanja današnje matematike in celo brez simbolnega zapisa reševali take in podobne naloge, pri tem pa so si pomagali s presenetljivim prepletom geometrije in algebre.
Kako računalnik naučimo igrati "4 v vrsto"?
Doc. dr. Branko Kavšek, UP FAMNIT in UP IAM
 Igro "4 v vrsto" zagotovo vsi poznamo. Ta igra za dva igralca je postala popularna v 80-ih letih prejšnjega stoletja, danes pa poznamo veliko najrazličnejših izvedb te igre, bodisi takih s pravim ogrodjem in žetoni, pa vse do različic za tablične računalnike. Prav tem računalniškim izvedbam, kjer enega ali pa kar oba igralca lahko nadomestimo z računalnikom, bomo posvetili posebno pozornost. Sprehodili se bomo skozi zgodovino te igre, spoznali pravila, si ogledali nekaj zmagovalnih strategij, jih zapisali v matematičnem jeziku in na koncu vse skupaj predstavili kot računalniški program. Ogledali si bomo tudi, kako računalnik učimo igrati to zabavno igro.
Igro "4 v vrsto" zagotovo vsi poznamo. Ta igra za dva igralca je postala popularna v 80-ih letih prejšnjega stoletja, danes pa poznamo veliko najrazličnejših izvedb te igre, bodisi takih s pravim ogrodjem in žetoni, pa vse do različic za tablične računalnike. Prav tem računalniškim izvedbam, kjer enega ali pa kar oba igralca lahko nadomestimo z računalnikom, bomo posvetili posebno pozornost. Sprehodili se bomo skozi zgodovino te igre, spoznali pravila, si ogledali nekaj zmagovalnih strategij, jih zapisali v matematičnem jeziku in na koncu vse skupaj predstavili kot računalniški program. Ogledali si bomo tudi, kako računalnik učimo igrati to zabavno igro.
Računanje z binomskimi koeficienti
Doc. dr. Matjaž Konvalinka, UL FMF
As. David Gajser, univ. dipl. mat., UL FMF
Znate dopolniti naslednji trikotnik?
Matrike, ki raztegujejo in vrtijo slike
Izr. prof. dr. Bojan Kuzma, UP FAMNIT

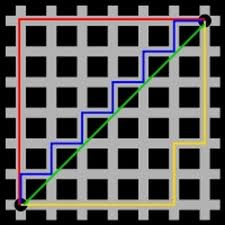
Zakaj je π=4 in druge zgodbe o razdaljah
As. dr. Boštjan Kuzman, UL PeF
Matematične igre in ukane
Prof. dr. Primož Potočnik, UL FMF in UP IAM

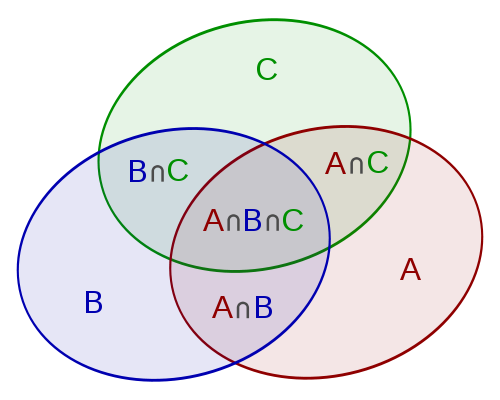
Zdaj si vključen, zdaj si izključen
Doc. dr. Primož Šparl, UL PeF
Kako zavarujemo skrivnosti pred starši?
As. dr. Jernej Tonejc, UP IAM
