Predavanja & delavnice

Internet stvari - prvi koraki, Andrej Brodnik, Nataša Mori

Koliko naprav imate doma, ki so ali jih lahko povežemo v Internet? Eno, mogoče dve? Ne, gotovo jih imate več, vsaj 10. Recimo, hladilnik, pečica, fotoaparat, avtomobil, rolete, garažna vrata, alarmni sistem, opazovalnik otroka, merilec srčnega utripa, termostat in še in še.
Kaj imajo te naprave skupnega? Vse imajo senzorje, ki zaznavajo spremembe, programe, ki z zaznanimi podatki nekaj počno, ter so običajno povezane v omrežje, preko katerega si izmenjujejo podatke. Hladilnik recimo zazna, katere izdelke imamo shranjene in nas opozori, ko zmanjka mleka; ali pa rolete se samodejno spustijo, ko je ura 8 zvečer, in se ponovno dvignejo naslednje jutro.
Na delavnici se bomo spoznali z mini računalnikom Raspberry Pi, na katerega bomo priključili senzorje ter lučke in motorčke. Računalnik bomo programirali v jeziku Python, da bo deloval kot vstopna točka za zajem podatkov za internet stvari. Še to, ne pričakujemo, da znate kakorkoli programirati – pričeli bomo povsem od začetka.
No, vroče nam tudi ne bo, saj bomo naredili preprosto klimatsko napravo. Kako? No o tem pa več na taboru! V izziv, premislite kakšno napravo bi si želeli in kako bi si želeli, da bi delovala – naj vaše ideje nimajo meja; razmišljajte na primer tudi o tem, da se lahko dve napravi med seboj pogovarjata oziroma sodelujeta.

Ako bi se Evklid rodil na Japonskem... - Bojan Kuzma

Origami je že zelo stara umetnost prepogibanja papirja. Metode origamija danes uporabljajo v avtomobilski industriji - kako zložiti zračno blazino, da se bo v primeru nesreče zanesljivo odprla? Prav tako jih srečujemo v vesolju in pri zlaganju zemljevidov. Pred kratkim so origami začeli preučevati tudi matematiki in odkrili nekaj presentljivih stvari. Z origamijem lahko na primer računamo: z njim z lahkoto rešimo nekatere geometrijske probleme, ki so z ravnilom in šestilom nerešljivi.

Ko krivulje oživijo - Boštjan Kuzman

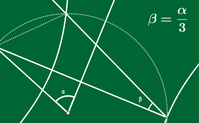Spoznali bomo nekaj klasičnih problemov, povezanih z geometrijo, kot so denimo Alhazenov problem zrcala, Arhimedovo kvadriranje parabole in Pappusovo tretjinjenje kota. Izbrane probleme in njihove rešitve bomo predstavili interaktivno s pomočjo programskega orodja GeoGebra. 

Matematika: od zapletene simbolnosti do preproste vsakdanjosti - Dragan Marušič

Čeprav so nekateri matematični izsledki v ozadju delovanja naše družbe, se matematika v vsakdanjem življenju večine posameznikov ustavi že pred uporabo štirih osnovnih računskih operacij. In na celi črti pogrne ob preprostih pravilih logičnega sklepanja. Povedano še nekoliko drugače: čeprav je matematika poleg materinega jezika edini predmet, ki se poučuje vse od prvega razreda pa do mature, pri marsikom vzbuja neugodje in odpor. Namen tega predavanja je pokazati, da matematika navkljub uporabi zapletenega simbolnega jezika posega tudi v prostor preproste vsakdanjosti.

Kaj vse lahko naredimo z ravnilom in šestilom? - Marko Orel

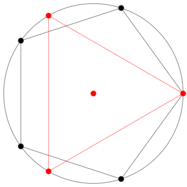Na predavanju bom poskusil odgovoriti na vpraššanja kot so na primer: Ali lahko s pomočjo ravnila in ššestila vsak kot razdelimo na 3 enake dele? Ali lahko dani kocki podvojimo volumen? Ali je "kvadratura kroga" možžna? Katere pravilne n-kotnike lahko nariššemo in kako to naredimo?


 

Grafi, igre in še kaj - Martin Milanič

prosojnice

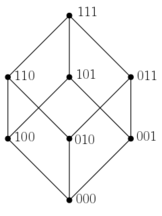Na predavanjih in delavnicah bomo spoznali osnovne definicije, leme in kakšen izrek področja matematike, imenovanega teorija grafov, zanimive aplikacije ter povezave z drugimi področji. Z grafi lahko obravnavamo številne raznolike probleme in igre, na primer:
1. Danih je n deklet in n fantov in relacija kompatibilnosti med njimi. Ali jih je možno razdeliti v n kompatibilnih parov?
2. Imamo dva kupčka z nekaj žetoni. Igralec na potezi mora z enega od kupčkov vzeti enega ali več žetonov. Zmaga igralec, ki vzame zadnji žeton. Kako poiskati zmagovalno strategijo v tovrstnih igrah?
3. Imamo n x n šahovnico, kjer ima vsak kvadrat stikalo in luč. Kadar pritisnemo na stikalo kvadrata, se spremeni stanje luči (ugasnjeno-prižgano) v tem kvadratu in v vseh sosednjih. Na začetku so vse luči ugasnjene. Ali je možno pritisniti na stikala kvadratov v takem zaporedju, da bodo na koncu vse luči prižgane?

Q.E.D. - Štefko Miklavič

Q.E.D. je okrajšava za latinski izraz "quod erat demonstrandum", ki pomeni "kar je bilo potrebno pokazati (demonstrirati)". Fraza oz. okrajšava zanjo se tradicionalno postavlja na konec matematičnih dokazov, v katerih je demonstrirana pravilnost določene (matematične) trditve. Primer take trditve je nam vsem dobro poznani Pitagorov izrek, ki trdi, da je v vsakem pravokotnem trikotniku vsota kvadratov dolžin katet tega trikotnika enaka kvadratu dolžine hipotenuze. Pa znamo tudi dokazati, da je to vedno res? V predavanju si bomo ogledali dokaze nekaterih najbolj znanih matematičnih trditev, ter preko njih spoznali različne vrste dokazov.

Matematika v ozadju igre SET - Vito Vitrih

Igra SET je igra s posebnim kompletom 81 kart. Vsaka izmed njih je določena s štiri lastnostmi, to so število, barva, oblika in polnilo simbolov na njej.
Cilj je poiskati tako imenovane SET-e, to je nabore treh kart, ki so si po vsaki izmed štirih lastnosti med seboj vse enake ali pa vse povsem različne. Na predavanju bomo spoznali trike iz verjetnosti in kombinatorike, ki nam lahko pomagajo pri razumevanju te igre in omogočijo, da imamo v primerjavi s soigralci večje možnosti za zmago.