Predavanja in delavnice

Dimenzija: od štetja do fraktalov - Blaž Mramor

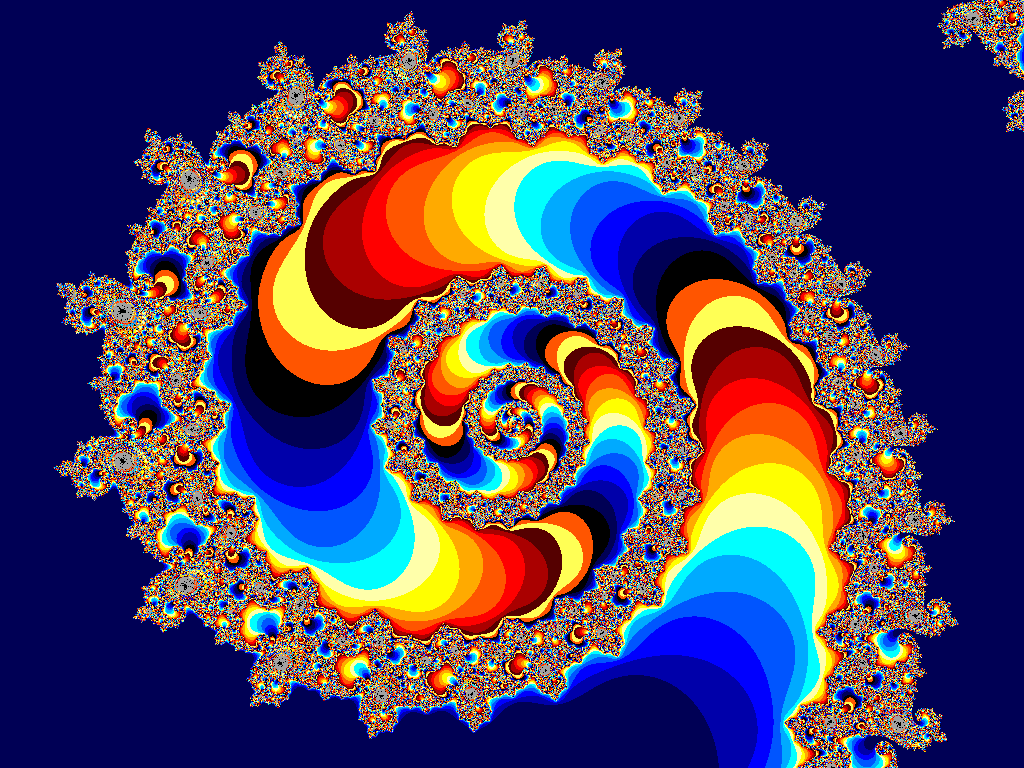Dimenzija je število, ki klasificira geometrične objekte v velikostne razrede. Na prvi pogled je pojem dimenzije enostavno razumljiv - da ima premica dimenzijo 1, ravnina dimenzijo 2 in prostor dimenzijo 3, je znano dejstvo. Nekoliko manj znano je, da v Einsteinovi teoriji relativnosti prostor in čas skupaj tvorita geometrični objekt dimenzije 4 (novejše fizikalne teorije govorijo celo o 11 in več dimenzionalnem prostoru), kvantno mehaniko pa se najlažje opiše z neskončno dimenzionalnimi prostori funkcij. Pri natančni definiciji dimenzije se hitro zapletemo in obstaja kar nekaj različnih definicij, ki med seboj ne sovpadajo vedno. Na prvi pogled se tudi zdi, da mora biti dimenzija vedno naravno število, vendar se v naravi pogosto pojavljajo geometrične strukture imenovane fraktali, za katere je smiselno dopuščati, da je njihova dimenzija lahko racionalno ali celo iracionalno število. Tipični primeri fraktaov so obrisi skalnatih obal (na primer obala Velike Britanije), rob praprotovega lista ali snežinke in bliski.

Matematika in šport - Boštjan Frelih

Že samo štetje in beleženje rezultatov, vodenje lestvic ter raznorazni statistični podatki, ki so prisotni, potrebni in koristni pri različnih športih, govorijo o tem, da je matematika v športu še kako prisotna. Predstavili bomo še nekatere primere uporabe matematike v športu in uporabo športa pri učenju in poučevanju matematike.

 

Iteracijske metode in numerična analiza - Jasna Prezelj

Ukvarjali se bomo z raznimi primeri iteracijskih metod, ki so jih matematiki v zgodovini uporabljali za izračun npr. kvadratnih korenov, sinusov majhnih kotov, ničel polinomov in podobno in poskusili kaj povedati o njihovi konvergenci. Pridobljeno znanje bomo uporabili za analizo logistične enačbe (enačba, s katero opisujemo rast populacij). Spoznali bomo tudi metode izračunavanja ploščine pod grafom (trapezna, Monte Carlo in druge). Zaključili bomo s praktičnimi primeri.

Od najmanjših kvadratov do delovanja CT naprave - Marko Orel

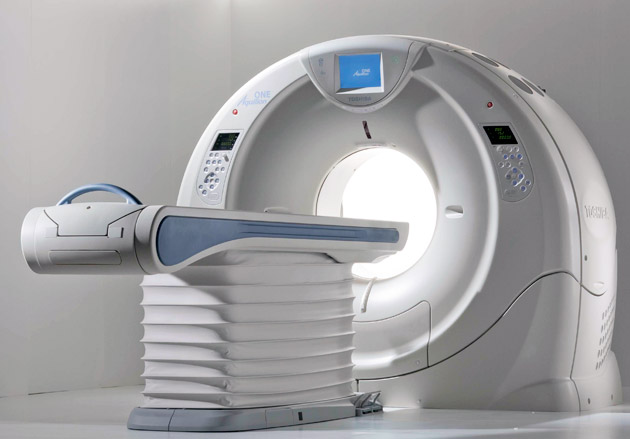Leta 1979 sta Nobelovo nagrado za fiziologijo ali medicino prejela Allan McLeod Cormack in Godfrey Newbold Hounsfield. Nagrada jima je bila podeljena za razvoj računalniško podprte tomografije v šestdesetih in sedemdesetih letih prejšnjega stoletja. Na predavanju bomo na poljudnoznanstven način prikazali matematiko, ki je bila zaslužna za delovanje prvega tomografa.

O Gaussovi krivulji - Martin Raič

Če naredimo histogram določene številske količine (npr. velikost, teža, tlak), dostikrat opazimo, da sledi obliki, ki je znana kot Gaussova krivulja. Spoznali bomo, zakaj in kdaj je temu tako. Najprej bomo to matematično izpeljali za met poštenega kovanca, nato pa bomo obravnavali še druge primere in opazovali, kako dobro se porazdelitev prilega Gaussovi krivulji. Spoznali bomo tudi, kdaj Gaussova krivulja ne pride v poštev. Ugotovitve bomo tudi ilustrirali z računalniškimi simulacijami.

Matematika delovanja spletnih brskalnikov - Rok Požar

Živimo v internetni dobi, kjer je dostop do informacij oddaljen le en klik. Preprosto odpremo spletni iskalnik, vtipkamo ključne besede in iskalnik nam vrne koristne rezultate. Toda kako spletni iskalniki zares delujejo? Na predavanju bomo na konkretnih primerih predstavili matematično ozadje njihovega delovanja in razvrščanja spletnih strani.

Izdelava zabavnih vsebin z otipljivim vmesnikom - Jernej Vičič

Otipljivi uporabniški vmesnik (Tangible User Interface) premošča prepad med fizičnim in digitalnim svetom. Izdelali bomo zabavno aplikacijo, igrico, ki bo sodelovala z uporabniki (igralci) s pomočjo dostopnega otipljivega uporabniškega vmesnika. Učenci spoznajo, kaj programiranje sploh je, preučijo nekaj enostavnih primerov iz vsakdanjega življenja in jih prenesejo v računalniško okolje. Seznanijo se z razvijalskimi okolji, ki omogočajo razvoj aplikacij, in z ogrodjem za igranje znane potezne igre 4 v vrsto. Skozi projektno timsko delo se seznanijo z osnovnimi strategijami igranja igre, izdelajo aplikacijo ter jo preizkusijo na popolnoma delujočem prototipu.

Zgodba s srečnim koncem - Istvan Kovács

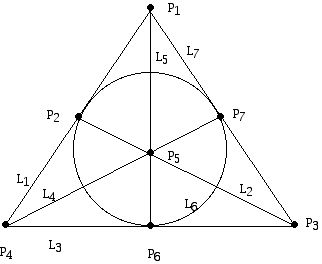Naša zgodba je prične z naslednjo šolsko nalogo: Zamislite si, da imamo pet točk v ravnini, tako da nobene tri ne ležijo na isti premici. Ali izmed teh petih točk vselej obstajajo štiri, ki tvorijo oglišča konveksnega štirikotnika? Odgovor je da, in take štiri točke lahko najdemo tako, da pogledamo konveksni poligon, generiran s petimi točkami. Leta 1933 je Eszter Klein zastavila naslednjo posplošitev zgornje naloge: Naj bo n celo število, večje ali enako 3. Ali obstaja tako število N(n), da med poljubno množico vsaj N(n) točk v ravnini, pri čemer nobene tri ne ležijo na isti premici, vedno lahko najdemo n točk, ki tvorijo oglišča konveksnega n-kotnika? Prejšnja naloga nam na primer pokaže, da je N(4)=5. Leta 1935 sta Pál Erdős and György Szekeres dokazala, da število N(n) obstaja za vsako celo število n, večje ali enako 3. Zgodba se je končala s poroko med Kleinovo in Szekeresom leta 1937, in zaradi tega je Erdős problem Klainove poimenoval "problem s srečnim koncem" ("happy ending problem"). Števila N(n) zanimajo matematike tudi dandanes. Na predavanju si bomo ogledali dokaz Erdősa in Szekeresa in obravnavali osnove pripadajoče Ramseyjeve teorije.

Skrivnostna sporočila - Ademir Hujdurović

Kako poslati sporočilo prijatelju, tako da ga nihče drug ne bo razumel? Kako pa prebrati šifrirano sporočilo? Kaj pomeni sporočilo "Nbufnbujlb kf lvm"? Na predavanju in delavnici bomo predstavili nekaj osnovnih modelov šifriranja sporočil ter metode za razkrivanje šifriranih sporočil.